精确对角化-以Bose Hubbard模型为例

发表于 分类于 阅读次数： Waline： 本文字数： 5.2k 阅读时长 ≈ 9 分钟

本文主要参照J M Zhang以及R X Dong一文精确对角化方法，以Bose-Hubbard模型为例，给出了对应的哈密顿量的构建方法。代码以matlab给出。

Bose-Hubbard模型

Bose-Hubbard模型指的是满足如下哈密顿量的模型：

\[\begin{equation} \hat{H}=-t\sum_{\langle ij\rangle}(a_{i}^{\dagger}a_{j}+a_{j}^{\dagger}a_{i})+\frac{U}{2}\sum_{i=1}^{M}\hat{n}_{i}(\hat{n}_{i}-1) \end{equation}\]

其中\(a_{i}(a_{i}^{\dagger})\)是湮灭(生成)一个在格点\(i\)上粒子的玻色算符，而数算符\(\hat{n}_{i}=a_{i}^{\dagger}a_{i}\)则计数在格点\(i\)上的粒子。由于该模型是玻色模型，每个格点上可以有多于两个粒子的共存。我们考虑有限个一维格点，假设总共有\(M\)个格点，若总原子数为\(N\)个，则总的Hilbert空间可以通过隔板法可以求得：

\[\begin{equation} D=\frac{(N+M-1)!}{N!(M-1)!} \end{equation}\]

可以发现该空间维数以指数增长。尽管可以通过对称性削减基的数量，在这里我们只考虑一个基础的数值方法，故在这里不作对称性分析。

本文的主要内容参考自相关文献[1]，给出了如何构建用于精确对角化的Bose-Hubbard模型的算法。为简便起见，这里采取周期性边界条件。

基的构建

由于我们需要考虑\(N\)个粒子分布在\(M\)个格点上的所有可能，尽管用循环的方式可以生成基，但其速度是相对慢的。事实上，对于Fock态，我们可以定义一个字典序(Lexicographic order)去排列所有的基。

给定两个Fock基向量\(|n_{1},n_{2},\cdots,n_{M}\rangle\)与\(|\bar{n}_{1},\bar{n}_{2},\cdots,\bar{n}_{M}\rangle\)，那么一定存在一个给定的编号\(1\le k\le M-1\)使得对于\(1\le i\le M-1\)有 \(n_{i}=\bar{n}_{i}\)，而\(n_{k}\neq \bar{n}_{k}\)。我们定义，若\(n_{k}\ge\bar{n}_{k}\)(\(n_{k}\le\bar{n}_{k}\))，则称向量\(|n_{1},n_{2},\cdots,n_{M}\rangle\)优于(superior)(劣于inferior)向量\(|\bar{n}_{1},\bar{n}_{2},\cdots,\bar{n}_{M}\rangle\)。可以证明，这样的序关系可以在基向量之间定义一个全序关系。此时明显有\(|N,0,\cdots,0\rangle\)优于其他所有基向量，而\(|0,0,\cdots,N\rangle\)劣于其他所有基向量。

借由这样构造的全序关系，我们可以从\(|N,0,\cdots,0\rangle\)以降序的方式生成其他所有占据数的基。给定一基向量\(|n_{1},n_{2},\cdots,n_{M}\rangle\)满足\(n_{m}<N\)，则我们生成劣于该向量的规则如下：

设\(n_{k}\neq0\)，且对所有的\(k+1\le i\le M-1\)都有\(n_{i}=0\)时，下一个基向量\(|\bar{n}_{1},\bar{n}_{2},\cdots,\bar{n}_{M}\rangle\)应当满足：

  • 当\(1\le i\le k-1\)时，有\(\bar{n}_{i}=n_{i}\)
  • \(\bar{n}_{k}=n_{k}-1\)
  • \(\bar{n}_{k+1}=N-\sum_{i=1}^{k}\bar{n}_{i}\)，且对于\(i\ge k+2\)有\(\bar{n}_{i}=0\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
% Initialize the basis through cell
Basis = repmat({zeros(1, N_Sites)}, Dimension, 1);
% Set the first basis as (N, 0, 0...)
Basis{1}(1) = N_atoms;
% Basis Generation
for ii = 2: Dimension
    % find the index of k
    Count = find(Basis{ii-1}(1:end-1)~=0, 1, 'last');
    temp = Basis{ii-1};
    if Count <= N_Sites - 1
        if temp(Count) ~= 0 && ~any(temp(Count+1:end-1))
            Basis{ii}(1:Count-1) = Basis{ii-1}(1:Count-1);
            Basis{ii}(Count) = Basis{ii-1}(Count) - 1;
        Basis{ii}(Count + 1) = N_atoms - sum(Basis{ii}(1:Count));
    end
    end
end
Basis = cell2mat(Basis);

通过这样的计算，我们可以得到所有的基，得到的Basis将是一个\(D\times M\)的矩阵，每一行代表一个基，而一个基的每个分量则代表这个格点上的占据数。

哈密顿量的构建

建立好基之后，便可以开始构建哈密顿量的分量：

\[\begin{equation} H_{uv}=\langle u|H|v\rangle \end{equation}\]

一般情况下我们需要的哈密顿量是稀疏矩阵，我们只需要找到对应的非零元。Bose-Hubbard哈密顿量分为两个部分，一个部分为动能跃迁项\(H_{\text{kin}}\)，另一个部分相互作用项\(H_{\text{int}}\)。因为在占据数表象下相互作用项是对角的，所以主要问题在于如何构建跃迁项。

一个直接的想法是将所有基向量都循环一遍——这个方法当然是可行的，但是当希尔伯特空间维数达到百万时，要遍历整个哈密顿量的矩阵所需要的时间是极久的。考虑到我们要写的动能项的哈密顿量形如\(a_{i}^{\dagger}a_{j}\)，由于这样的跃迁总是近邻跃迁(例如一维情况下，考虑\(M>3\)个格点，则格点2上有从\(2\to 3\)和\(2\to1\)两种跃迁)，对于\(M\)个格点而言，最多只有\(2M\)个跃迁项，于是一个更简单的方法是，首先将基排好序，然后给定一个对应于哈密顿量第\(v\)列的基向量\(|v\rangle\)，找到动能项哈密顿量作用在基上后的两个跃迁后的基，再乘上跃迁系数，就得到了对应的非零项，而这两个基对应的序列则给出了哈密顿量非零元的行指标。例如考虑一个5格点3个粒子的情形，给定基\(|0,3,0,0,0\rangle\)，该向量的两种跃迁为\(|1,2,0,0,0\rangle\)或\(|0,2,1,0,0\rangle\)，则对应的哈密顿量第\(v\)列的非零行就是这两个基的位置。然后再遍历所有列，就可以写出动能部分哈密顿量。通过上面的方法，问题被转化成了如何找到经过哈密顿量作用后的非零向量所处的序列，这对应到哈密顿量的行列指标。

在对应非零基向量时，相比于挨个挨个地对应值，我们可以利用一种哈希技术(Hashing technique)来更快地找到对应地向量。简单来说，哈希算法给每个基向量都定义一个标签(Tag)，从而要比较两个向量是否相同时，只需要比较他们的标签是否一致即可。

由于我们在生成基向量的时候已经定义了字典序，我们在这里可以进一步的利用字典序来定义一个标签函数。一个可选方案是：

\[\begin{equation} T(|v\rangle)=\sum_{i=1}^{M}\sqrt{p_{i}}v_{i} \end{equation}\]

其中\(p_{i}\)可以是第\(i\)个质数。由于matlab的prime函数生成质数的速度不快，可以参考文章[1]中直接可以使用\(p_{i}=100i+3\)。

在给基编好号之后，为了更快地查找，还可以通过tag值对基向量进行排序，这样可以利用二分法进行查找，从而对于\(D\)个基向量，要找到对应的向量只需要\(\log_{2}D\)次寻找。

1
2
3
Tags = Basis * sqrt(100 * (1: N_Sites) + 3)';
% Sort the Tag function
[Tags, ind] = sort(Tags);

这样一来，最后就只需要找到对应的非零元的行列以及对应的值，就可以利用sparse命令建立动能部分哈密顿量。对应的matlab代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
for ii = 1: Dimension
    ind_nonzero = find(Basis(ii,:));
    for jj = 1: length(ind_nonzero)
        % Nearest hopping
        % Left hopping matrix element
        temp = Basis(ii,:);
        temp(ind_nonzero(jj)) = temp(ind_nonzero(jj)) - 1;
        temp_site = ind_nonzero(jj) - 1;
        if temp_site == 0
            temp_site = N_Sites;
        end
        temp(temp_site) = temp(temp_site) + 1;
        temp_Tag = temp * Tag_function(N_Sites)';
        col(Count) = ii;
        row(Count) = ind(abs(Tags - temp_Tag) < Accuracy);
        val(Count) = sqrt(Basis(ii,ind_nonzero(jj)) * (Basis(ii, temp_site)+1));
        Count = Count + 1;
        
        % Right hopping matrix element
        temp = Basis(ii,:);
        temp(ind_nonzero(jj)) = temp(ind_nonzero(jj)) - 1;
        temp_site = ind_nonzero(jj) + 1;
        if temp_site == N_Sites + 1
            temp_site = 1;
        end
        temp(temp_site) = temp(temp_site) + 1;
        temp_Tag = temp * Tag_function(N_Sites)';
        col(Count) = ii;
        row(Count) = ind(abs(Tags - temp_Tag) < Accuracy);
        val(Count) = sqrt(Basis(ii,ind_nonzero(jj)) * (Basis(ii, temp_site)+1));
        Count = Count + 1;
    end
end
H_kinetic = sparse(row, col, val);

这里采取的方法是，给定一个基向量\(|v\rangle\)记为列指标，仅对于其占据数非零的格子进行遍历，然后分别考虑向右跃迁和向左跃迁的情况，并找到对应的向量指标记为行指标，同时将其跃迁带来的值进行记录，最后利用sparse命令生成即可。

注意在多粒子体系中有：

\[\begin{equation} a_{i}^{\dagger}a_{j}|v\rangle=\sqrt{(v_{i}+1)v_{j}}|\cdots,v_{i}+1,\cdots v_{j}-1,\cdots\rangle \end{equation}\]

会带来额外的粒子系数。

最后则是对角的相互作用部分，可以轻易地用一行指令写下：

1
H_interaction = spdiags(sum(Basis .* (Basis - (Basis>0)),2), 0, Dimension, Dimension);

合在一起，便得到了Bose-Hubbard模型的哈密顿量：

1
2
H = -t * H_kinetic + U/2 * H_interaction;
spy(H)
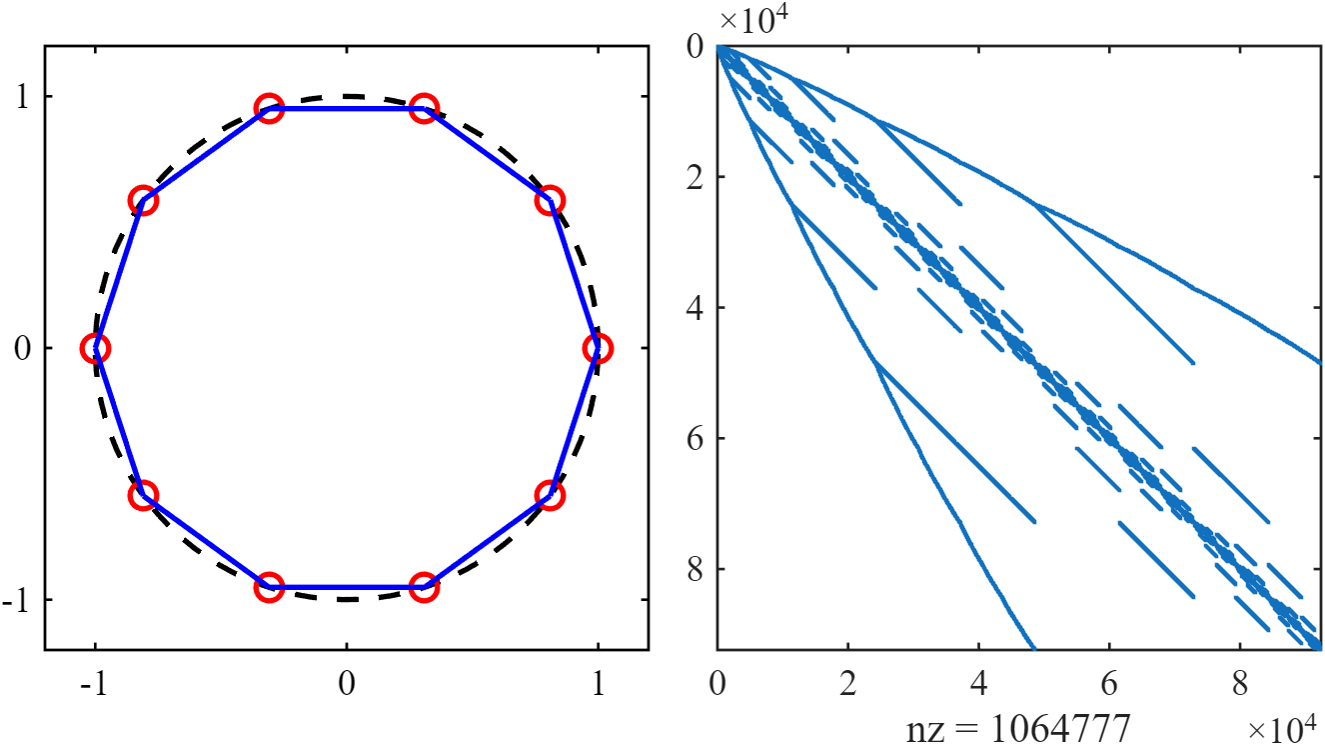alt text
左图为M=10且N=10的格点图，右图为对应的哈密顿量的稀疏矩阵
  1. 1.J M Zhang and R X Dong. Exact diagonalization: The Bose–Hubbard model as an example. European Journal of Physics, 31(3):591–602, May 2010. ↩︎