杂谈-什么是物理图像？
引论
通常在学物理/做物理的人之间会有一个专有名词叫物理图像(Physical Picture)，有时也简称为物理。例如交流的时候会说"你这篇文章的物理(图像)是什么"。然而维基百科上并没有关于这个词的明确定义，且在不同的语境下物理图像指代对象会有极大的不同。为了能够理清这一词至目前的各种含义，于是便写下了这篇杂谈。
物理模型
作为自然学科的基础之一，物理的核心在于研究自然。而要研究自然，目前最有效的方式是根据现实提取出对应的物理模型进行分析。
为了得到响应的物理模型，在考虑现实中的各种物理对象时，首先要对该对象进行抽象，以此得到最简单而又最能反应所关注的内容的一个物理模型.例如质点这一对象是对任意不关注其大小以及形状的物体的抽象，这一抽象对象在研究一个物体的运动，尤其是空间上的平移时时最为有效，因为我们只需要关注质点在空间中的位置即可。然而由于抽象过程中我们抛弃了太多信息，导致其缺点在于质点是一个没有大小的点，我们没有办法研究它的旋转。
若是要研究旋转，我们需要加入一些关于形状和大小的细节，这个时候将刚体的抽象要更加有利于研究。借此我们可以研究对象的旋转。若是要研究刚体在各种受力下的变化，我们就需要加入更多的细节，例如物体可以发生形变，扭曲，断裂，拼接，融合等各种现实中存在的过程。无论如何，在研究自然时，我们总是需要根据研究对象去提取出当前对象最关键的信息，通过抽象来建立一个物理对象的模型，这便是物理模型。
数学模型
在建立了物理模型后，我们需要描述其各种关心的性质以及各种性质之间的联系。而目前最好的描述工具是数学，在基于对应的物理模型的基础上，进一步用数学建立的模型可以称为数学模型。或许最广为人知的数学模型应当是牛顿的运动学第二定律 \[\begin{equation} \mathbf{F}=m\mathbf{a} \end{equation}\] 这个公式描述了一个真空中质量为\(m\)的物理对象受到的力\(\mathbf{F}\)与其因力而产生的加速度\(\mathbf{a}\)的关系，这是一个数学函数关系，因此可以认为其是一个描述任一满足特定假设[1]下用于描述物理模型的数学模型。 这个数学模型的特殊性在于，与其他任意\(y=f(x)\)相比，当我们将这三个变量(两个是矢量)中任意两个变量换为任意物理对象的对应的已知参数的数据[2]时，求解得到的第三个未知的变量的数据将必然与在现实中的物理对象通过实验测得的数据在一定的误差范围内相同。这一重要区别使得一个物理模型所对应的数学模型具有了一定程度的预测现实的功能。
物理理论
在阐明了物理模型以及的对应的数学模型后，便可以开始讨论物理理论。一个物理理论是一类物理事件的模型。由于对现实的一对一建模是不可能的事情，因此人们更希望通过一系列有限的物理模型来提取出一个(或一类)更加本质的模型，当遇到全新的对象时，直接利用这个本质的模型去套用即可分析新的对象，这就是物理理论。它的评判标准是其预测与实证观察的一致性程度。物理理论的质量还取决于它做出新预测的能力，这些预测可以通过新的观察来验证。这一套采用数学模型和物理对象和系统的抽象来合理化、解释和预测自然现象[3]对应为理论物理学。亦即，理论物理学是研究物理理论的学科。
对于物理理论的描述，通常是利用数学模型来描述一类物理模型的性质以及其之间的关系。一个物理理论通常会包含多个物理模型以及其对应的数学模型。例如牛顿力学便是一个物理理论，其包含了质点、刚体等多个物理模型，以及对应的牛顿定律等数学模型。
然而，以纯粹物理理论的严格性和信息量而言，要想直接对其进行讨论是非常困难的。因此，通常人们会在讨论物理理论时，使用物理图像来进行描述。在这之前，需要对图像这个词进行一些意义的拓展
图像
图，或者图像，是一般人每时每刻都需要的一种信息。借用维基百科的介绍[4]， > 图像或图片是一种视觉表示形式。图像可以是二维的，例如绘图、绘画或照片，也可以是三维的，例如雕刻或雕塑。
作为含有信息量最丰富的对象，其直观与简洁对于理解事物具有极大的帮助性。例如描述圆的时候，数学上通常用解析几何的方法，来定义满足方程
\[\begin{equation}
x^2+y^2=r^2
\end{equation}\] 的点集(x,y)构成的集合，而图像上可以很简单的给出
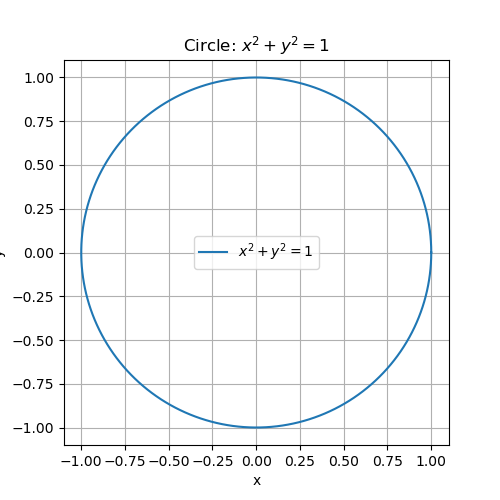从这个角度来说，图像作为信息的载体，其特征在于简洁与直观。
## 物理图像
在介绍完了物理模型和图像后，物理图像简单来说便是指一类简洁直观的物理模型。需要注意的是，物理图像并不指代物理实在，而是指一个方便理解的抽象对象。因为只有在有了对象之后，才可以谈及对象之间的关系，也即物理关系。而所谓常说的"新物理"，也是指一类新的物理图像以及其对应的之前所未探明的物理关系。
总结
物理图像作为一种简洁直观的物理模型，其主要是在简单的讨论中，避免涉及过多的计算但是却能理清复杂的物理关系的工具。利用物理(图像)，即便是不甚了解一个理论内部的数学关系，也可以理清楚不同物理对象之间的关系，这极大的降低了交流成本。除此之外，物理图像的重要意义在于，通过考察物理图像对应的自然现实，有时甚至可以跳过严格的数学构造和推导，直接抽取出可能的物理关系。例如已知牛顿第二定律是一个二阶微分方程，对于匀速运动而言其解需要首先求解该微分方程，得到解 \[\begin{equation} \boldsymbol{s}=\frac{1}{2}a t^2+bt+c \end{equation}\] 然后带入初始条件，计算后才能得到 \[\begin{equation} \boldsymbol{s}=\boldsymbol{v}t+\boldsymbol{s}_0 \end{equation}\] 但是，如果直接考虑一个匀速运动的物体，我们应当可以很轻易地直接写下 \[\begin{equation} \boldsymbol{s}=\boldsymbol{v}t+\boldsymbol{s}_0 \end{equation}\] 这种方法甚至在分数量子霍尔效应中诞生过诺贝尔奖，其得主Robert Laughlin在没有任何数学推导的情况下，直接写出了分数量子霍尔效应的物理图像，并且成功地解释了实验结果。
题外话
作为一个个人的观点，实际物理学中的解释并非对现实行为的解释，而是基于物理图像的对物理模型的解释。因为现实世界是极其复杂的，如果一个理论能够解释现实，那么现实就不应该存在无法解释的对象，然而客观上现实中存在无法利用理论解释的现象，这实际上正是物理理论作为物理模型的集合的局限性所在。而所谓的解释，实际上是基于物理模型对该框架下的可能的物理图像的解释[5]。
- 1.牛顿定律仅在低速宏观领域下成立，当关注的对象处于高速宏观领域时，我们需要用到相对论力学，而处于低速微观领域时需要量子力学，处于高速微观领域下则需要量子场论。 ↩︎
- 2.之所以是数据而非数字，在于单位。 ↩︎
- 3.见WikiPedia 理论物理学 ↩︎
- 4.见WikiPedia 图片 ↩︎
- 5.本文中部分论述使用copilot润色。 ↩︎