恒星的流体静力学平衡

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 6k 阅读时长 ≈ 10 分钟

前言

作为第一篇非叙事的文章，总是要有一些精彩的内容的。思来想去，还是认为只有Steven Weinberg (物理学家，诺贝尔奖获得者)的著作Lectures on Astrophysics(天体物理学讲座)的第一节足够精彩。

这本书全册共226页，当然是塞不下天体物理的主要内容的。相反，作者意在给出一些在无需计算机帮助下，依然能展现出一些与真实世界相关的天体物理相关的简单计算。

...Instead, I here offer a short course, a collection of astrophysical calculations that can be done simply and analytically, without recourse to computers, and yet are relevant to the real world....

本书的第一节-Hydrostatic Equilibrium(流体静力学平衡)仅只需要基础的微积分知识和万有引力定律，再加上一些热力学概念，便给出了许多精彩的结论。 # 恒星的引力平衡 宇宙中的恒星[1]通常都是稳定的发光体，所以可以假定星体是一团由引力凝聚在一起的稳定的物质。由于万有引力只依赖于物质之间的距离，可以近似认为恒星是球形的，也即具有球对称结构。因此，采取球坐标系分析是较为方便的。 回想万有引力定律 \[ \begin{equation} F=-G\frac{Mm}{r^2} \end{equation} \] 既然引力是万有的，那么自然在恒星内部之间也是存在引力的。星体内部的物质为了平衡这样的引力维持稳定的结构，必然产生一定的压力。我们的出发点便是基于这样的一个平衡-一个稳定存在的恒星，其内部之间的引力应当与物质因过于紧密而产生的压力相等。

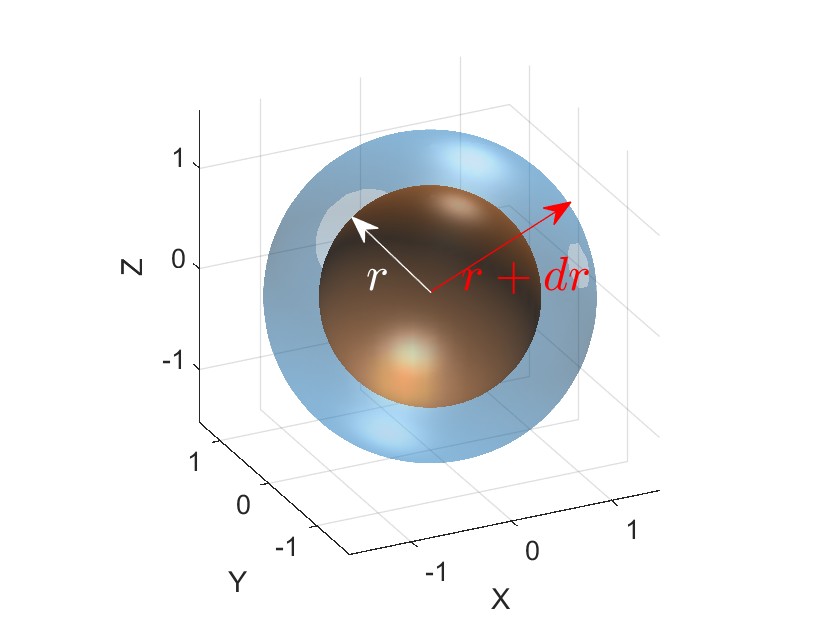PlotofStar 如上图所示，我们假设星体的密度是半径的函数\(\rho(r)\)，那么半径为\(r\)的恒星内部球体的质量就是

\[ \begin{equation} \mathcal{M}(r)=\int_0^r 4\pi r'^2\rho(r')dr'. \end{equation} \]

对应的，这个球体对其外部厚为\(dr\)的球壳(可以验证，这个球壳的质量是\(4\pi r^2 \rho(r)dr\))所产生的引力对应为[2] \[ \begin{equation} F_{\text{引力}}=-G\frac{\mathcal{M}(r)\times 4\pi r^2 \rho(r)dr}{r^2}=-4\pi G\rho(r)\mathcal{r}dr \end{equation} \] 这里的负号代表引力总是指向球心的方向。接下来考虑压力导致的浮力(正如物体在水中所受到的浮力是由于物体底部接收到的压强要大于物体顶部收到的压强，这对于恒星也是成立的!)。假设在半径\(r\)处的压强为\(p(r)\)，由于球壳内侧的压强要大于球壳外侧的压强，我们可以计算出它的压强差导致的浮力为 \[ \begin{equation} F_{\text{浮力}}=4\pi r^2\left[p(r)-p(r+dr) \right]=-4\pi r^2 p'(r)dr \end{equation} \] 由于恒星是稳定的，故对恒星内任意这样的球壳，其受到的引力都应当与受到的浮力相当，所以我们可以联立这两个方程，经过简单的化简，可以得到 \[ \begin{equation} \label{eq:hydrostatic} \boxed{\frac{dp(r)}{dr}=-\frac{G\mathcal{M}(r)\rho(r)}{r^2}} \end{equation} \] 该公式给出了星体内部任一半径处的压力与质量的关系，这就是恒星的流体静力学平衡下的基本方程(Fundamental equation of hydrostatic equilibrium for stars)。

恒星的引力势能

在讨论恒星的能量前，我们需要回想一下如何定义能量。回想高中的物理知识，一个静止的物体的物体的动能可以通过对其施加外力造成位移来增加，也即通过做功来增加物体的能量 \[ \begin{equation} W=\int \vec{F}\cdot d\vec{x} \end{equation} \]

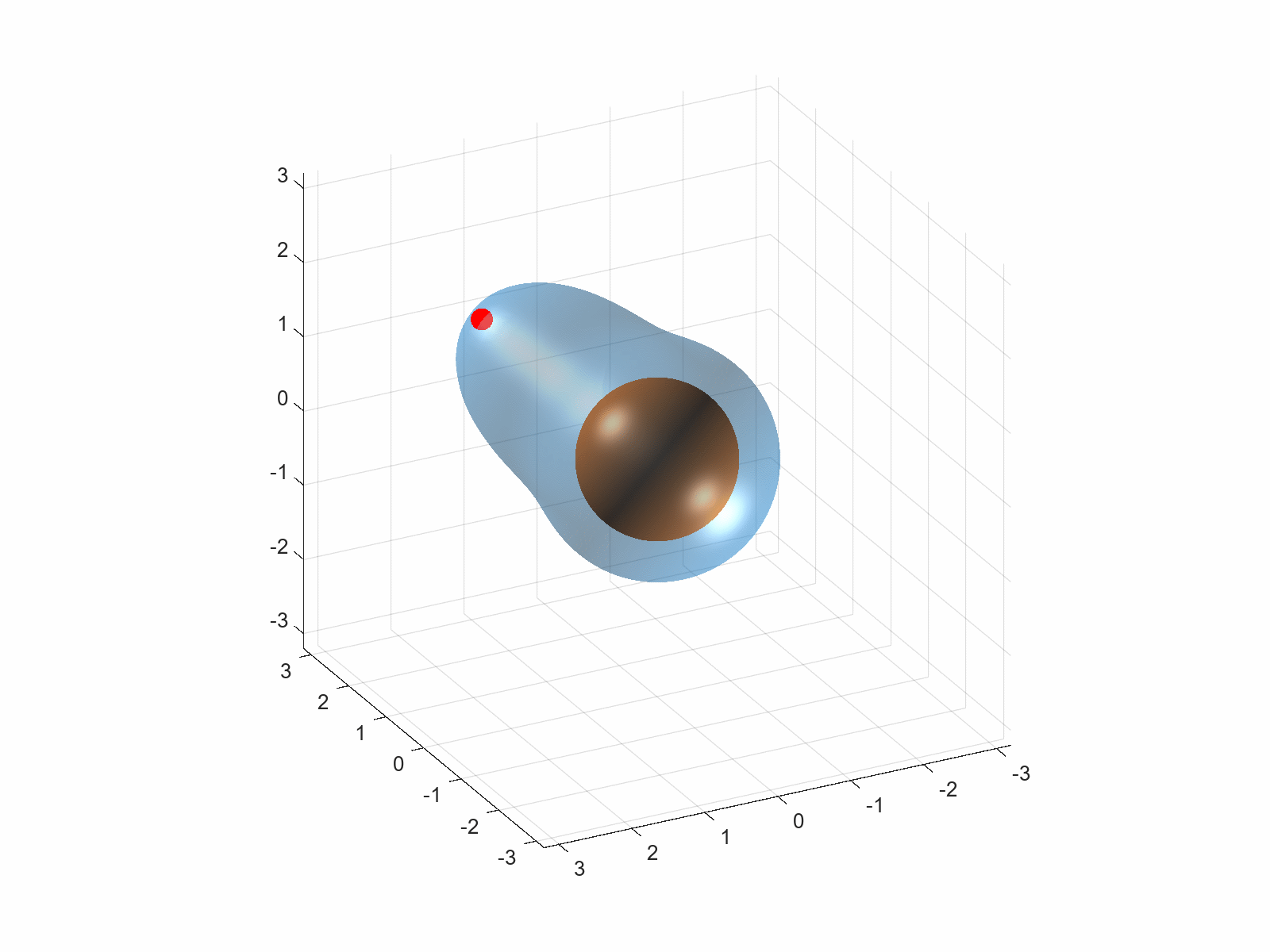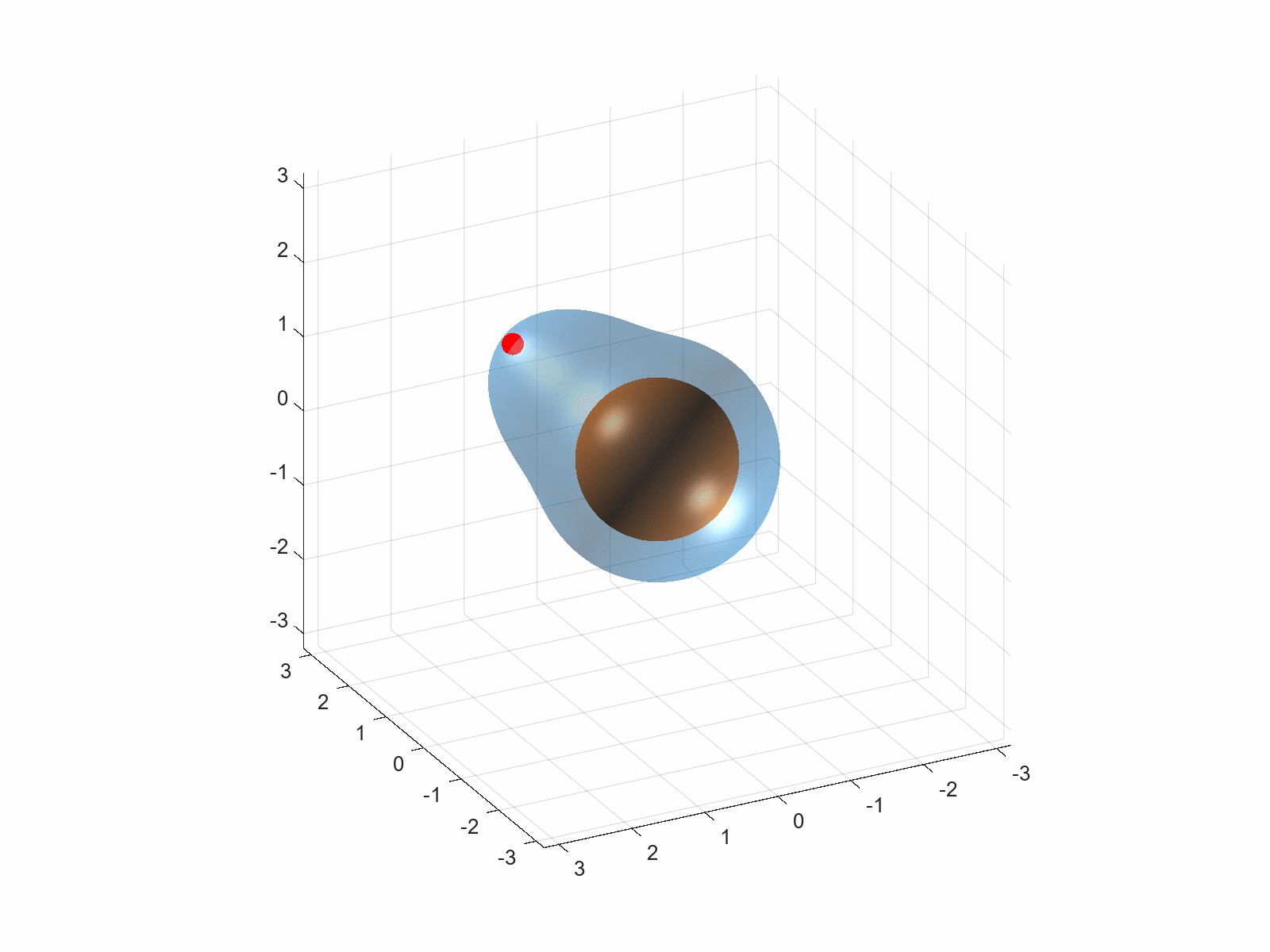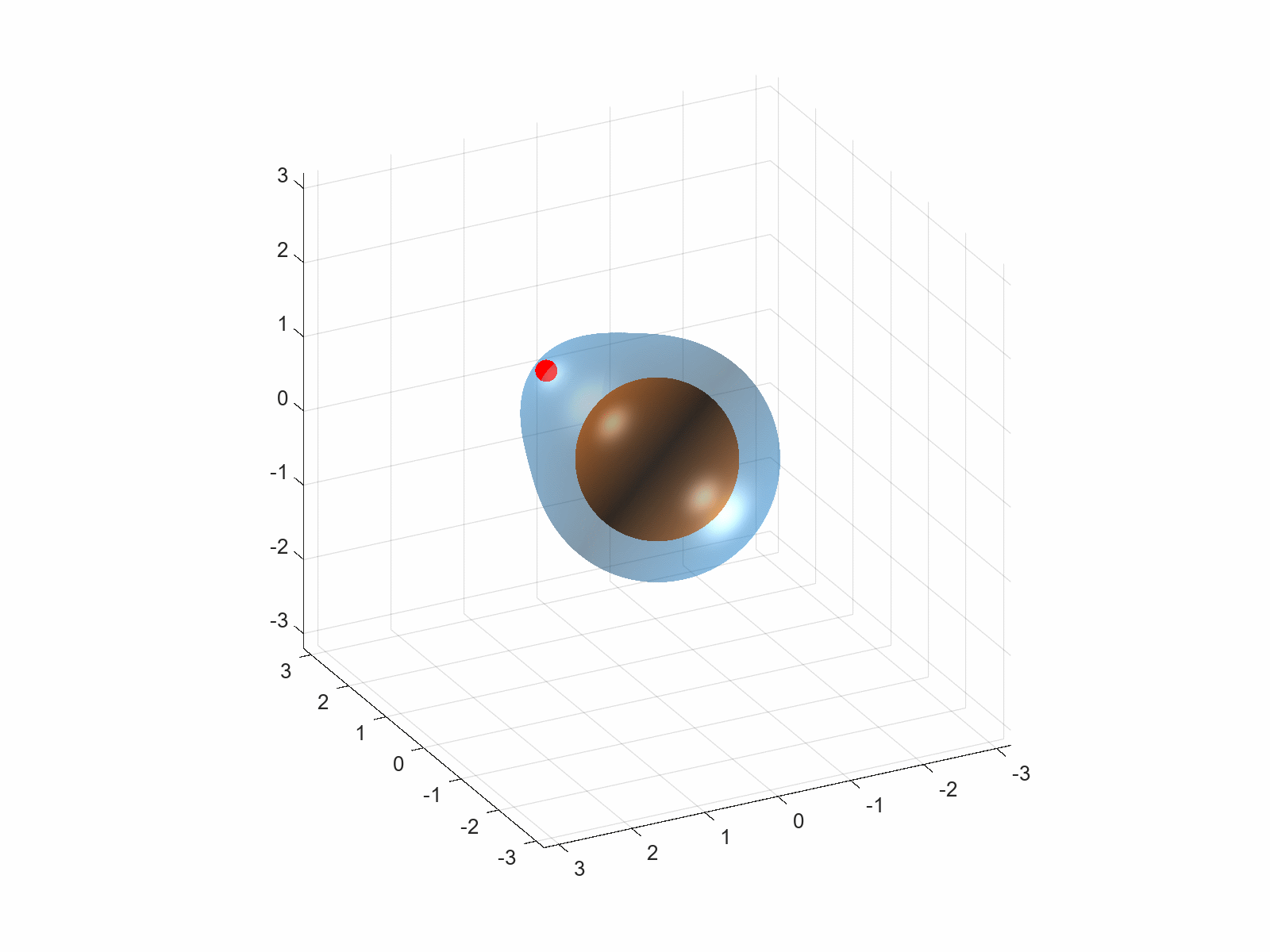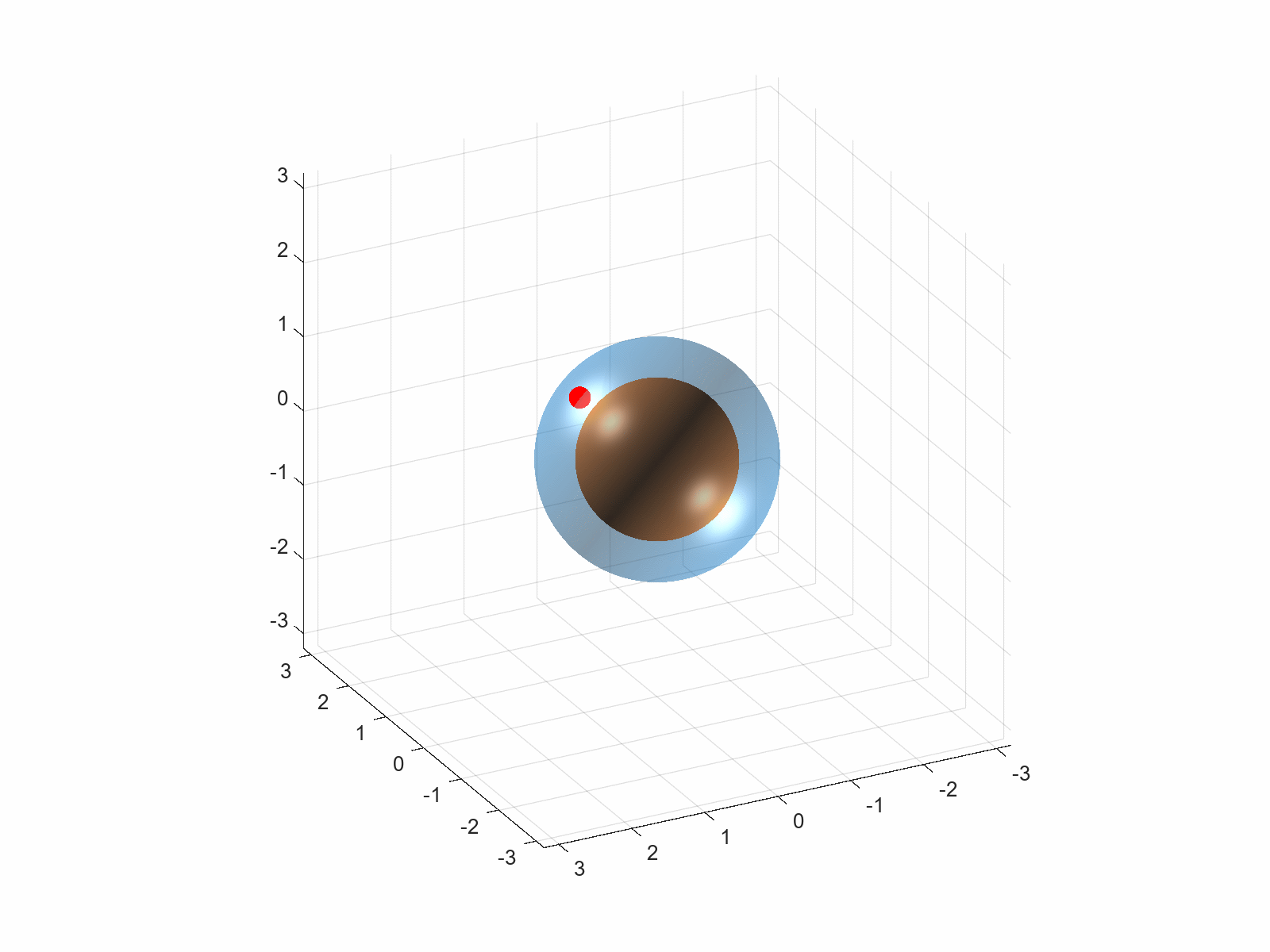
现在对于恒星而言，我们要考虑的从动能变成了引力势能，也即需要考察来自无穷远处的物质因引力而聚集在一起时，引力所做的功。由于恒星可以认为是个球，我们采取与上面相同的讨论，即通过讨论包裹在球体外的薄球壳，从无穷远到球体表面所累积的引力势能，来求得整个恒星所具有的引力势能，如下图所示(仅展示了一个球壳上的一个微元，即图中的红点) PlotofStarFallen

可以验证，半径为\(r\)的质量为\(\mathcal{M}(r)\)的星体产生会产生的引力为\({\color{blue}G\mathcal{M}(r)/r^2}\)，而其将无穷远处的物质吸引到球表面，形成一层质量为\({\color{brown}4\pi r^2\rho(r)dr}\)的球壳所做的功为 \[ \begin{equation} \int_{r}^{\infty}{\color{blue}G\mathcal{M}(r)/r^2}\times{\color{brown}4\pi r^2\rho(r)dr} \times{\color{red}\frac{1}{r'^2}dr'}=4\pi G r\mathcal{M}(r)\rho(r)dr \end{equation} \] 注意区分开标红的被积分半径\(r'\)与表示球壳所在的半径\(r\)!前者是因为，在将球壳从无穷远移动到球面上时，球壳所受到的引力也会随距离变化(万有引力告诉我们，这个力平方反比于二者的距离)，我们需要对其作积分；而后者代表我们所关注的球壳的半径。

现在已经求得了半径为\(r\)的球体吸引球壳所需要的功，我们再对整个半径作积分直至整个恒星的半径即可得到恒星的引力势能 \[ \begin{equation} -\Omega=4\pi G\int_0^{\color{red}{R}} r\mathcal{M}(r)\rho(r)dr \end{equation} \] 这里\({\color{red}{R}}\)为恒星的半径，一般而言这个半径定义为恒星的压强为0的地方，即\(p(R)=0\)(类比地球的大气层内的一个大气压，而在大气层之外则接近为0).公式左侧即为恒星的引力势能\(\Omega\)，注意前面的负号，因为引力总是相互吸引的，而在引力做功的时候，被吸引的球壳本应该将获得的引力势能转化为动能，而我们在计算球壳从无穷远到星体表面时默认了这个球壳会不带有动能地直接落在球面上形成了稳定的恒星[3]，而作为代价，我们得到的引力势能应当为负。

现在是时候回顾公式\(\eqref{eq:hydrostatic}\)了。利用该公式，我们可以将上式重新写为 \[ \begin{equation} \Omega=4\pi \int_0^R\frac{dp(r)}{dr}r^3dr=-3\int_0^R p(r)4\pi r^2 dr \end{equation} \] 注意为得到这个等式，需要利用分部积分以及\(p(R)=0\)来消掉分部积分带来的\(r^3p(r)|^R_0\)因子。

恒星的能量

现在已知了恒星的引力势能，实际上恒星内部还有热能\(\Upsilon\)[4]（又经常叫做内能）.其形式可以写为单位体积能量密度的积分

\[ \begin{equation}\label{innerenergy} \Upsilon=\int_0^R\mathcal{E}(r)4\pi r^2dr \end{equation} \] 其中\(\mathcal{E}\)是不包括恒星的质能\((E=mc^2)\)或引力能的内能密度。接下来我们可以将恒星的非相对论的能量写下

\[ \begin{equation}\label{energy} E=\Upsilon+\Omega=\int_0^R\left[\mathcal{E}(r)-3p(r)\right]4\pi r^2 dr \end{equation} \] 从被积部分可以看到，若\(\mathcal{E}(r)-3p(r)<0\)，此时恒星的引力势能大于内能，从而可以使整体能量为负，也即恒星吸引在一起。

多方球假设

为了更进一步地讨论恒星的能量，在这里稍微离题一下，我们需要给出一些热力学知识来建立恒星的压强与能量的关系。

通常而言我们可以假设内能与压强的关系为 \[ \begin{equation}\label{polytrope} \mathcal{E}(r)=\frac{p}{\Gamma-1} \end{equation} \] 这个关系叫做多方球假设，其中额外的参数\(\Gamma\)叫做绝热指数。为了更进一步地说明这个关系，我们可以拿高中的理想气体举例子。高中接触过的理想气体状态方程 \[ \begin{equation} pV=Nk_{B}T \end{equation} \] 其中\(p\)为压强，\(V\)为气体体积,\(k_B\)是玻尔兹曼常数，\(N\)为气体的原子数，\(T\)为温度。如果我们用单位体积数密度\(n=N/V\)，则上式可以写为 \[ \begin{equation}\label{eq:idealgas} p=nk_{B}T \end{equation} \] 在热力学上可以证明，此时我们可以计算出理想气体的能量密度为 \[ \begin{equation} \mathcal{E}={\color{red}\frac{3}{2}}nk_{B}T \end{equation} \] 注意前面的系数!实际上利用\(\eqref{eq:idealgas}\)可以得到\[ \begin{equation} \mathcal{E}=\frac{3}{2}p=\frac{p}{5/3-1} \end{equation} \] 所以对于理想气体而言，我们有 \(\Gamma=5/3\) .除了理想气体之外，对于辐射而言(不再是由普通的有质量原子构成的气体，而是由无质量的光子构成的气体)有 \(\mathcal{E}=3p\) 从而 \(\Gamma=4/3\).

恒星的爆炸

在建立了内能函数与压强的关系后，我们终于可以来讨论恒星的爆炸了！利用\(\eqref{polytrope}\),\(\eqref{innerenergy}\)和\(\eqref{energy}\)，我们可以建立一个简单的代数关系 \[ \begin{equation} \begin{split} E&=\Upsilon+\Omega=\int_0^R\left[\mathcal{E}(r)-3(\Gamma-1)\mathcal{E}(r)\right]4\pi r^2 dr\\ &=(4-3\Gamma){\color{brown}\int_0^R\mathcal{E}(r)4\pi r^2 dr}=(4-3\Gamma)\times{\color{brown}C}\\ \Upsilon&={\color{brown}\int_0^R\mathcal{E}(r)4\pi r^2 dr}={\color{brown}C}\\ \Omega&=E-\Upsilon=3(1-\Gamma){\color{brown}C} \end{split} \end{equation} \] 这意味着，恒星的总能量，引力势能以及内能满足如下的简单的代数关系 \[ \begin{equation}\label{eq:Explode} \boxed{\Upsilon=-\frac{E}{3\Gamma-4},\quad\Omega=\frac{(\Gamma-1)E}{\Gamma-4/3}} \end{equation} \] 当总能量\(E\)为正值时恒星将发生爆炸，因此要维持稳定需满足\(E < 0\)。可是由于引力势能总是小于零，即\(\Omega<0\)，从上式的第二个方程可以看出，我们必须要有\(\frac{\Gamma-1}{\Gamma-4/3}>0\),这给出 \(\Gamma<1\) 或 \(\Gamma>4/3\) .根据上面的热力学讨论，\(\Gamma\)通常都是大于1的，从而我们必然有\(\Gamma>4/3\).实际上，对于压强主要由高度相对论性粒子主导的天体（例如质量接近理论上限的大质量普通恒星、白矮星和中子星），其\(\Gamma\)值仅略高于4/3，说明这类天体的稳定性实际上已经很差了。

方程\(\eqref{eq:Explode}\)在恒星早期演化过程中起着决定性作用。一团低温弥散气体云内部的引力能和内能极低，其总能量\(E\)值很小。只要该气体云未处于绝对零度，就会持续辐射出以红外波段为主的光线。若其总能量转为负值，气体云便无法继续扩散。根据方程\(\eqref{eq:Explode}\)，只要绝热指数\(\Gamma>4/3\)，气体云在损失能量的过程中，尽管总能量\(E\)持续减小（负值越来越大），但其内能\(\Upsilon\)却会不断增大，也即恒星此时表现出负比热特性：恒星能量损失越多，温度反而越高。随着温度上升，恒星能量辐射的速度又进一步加快，这一过程形成正反馈循环。最终当恒星核心温度高到足以克服原子核间的库仑斥力时，核聚变反应启动并持续增强，直至核能产出与辐射损失达到平衡，恒星便进入稳定阶段（至少在其核心核燃料耗尽前会保持稳定）。看似矛盾的是，核反应的发生反而中止了恒星的持续升温过程。

  1. 1.通常所说的星体(Stars)都代指恒星，而非像地球这样的岩石行星(Rocky planet)，因为夜空中能够肉眼可见的星体几乎都是能够通过核反应自发光的恒星。 ↩︎
  2. 2.注意，这里我们利用了引力的一个性质，即一个球体对位于其外部的物体所施加的引力，等效于位于该球体球心的具有相同质量的质点对该物体所施加的引力。这个性质使得我们考虑内部球体对球壳所施加的引力时，不需要考虑内部球体的任一点对球壳施加的压力，直接将距离替换为球心到球壳的距离即可。 ↩︎
  3. 3.实际上这关系到恒星的形成过程。恒星整体上而言是星际间物质由于引力而相互吸引，这个时候引力势能转化为的动能非常大，从而导致星际物质之间会发生碰撞与摩擦，在这个过程中动能会转化为热与辐射离开这个体系，从而减少了动能。并且即便有这样的一个过程，在形成恒星后这些动能也并未完全被消耗掉。 ↩︎
  4. 4.这个符号是希腊字母Upsilon，与原文保持一致 ↩︎